La salida de resultados es:
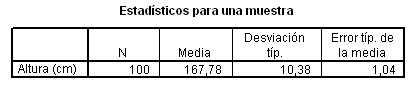
Prueba para una muestra

Por tanto vemos que en nuestra muestra la media para la v.a altura es de 167.78 cm con un EE de 1.04. Sabemos que la media poblacional es de 162 cms y es el valor a compara que introduce en la caja "valor de prueba". En la segunda tabla vemos que la significación es < 0.05, por tanto hay diferencias significativas. La diferencia entre ambas medias es de 5.78 cm y para esta diferencia se establece un intervalo de confianza al 95% que va desde 3.72 cm a 7.84 cm.
3. PRUEBA T PARA DOS MUESTRAS INDEPENDIENTES
Con esta prueba contrastamos la hipótesis de que las medias de dos poblaciones independientes son iguales. Generalmente la hipótesis nula que se contrasta es la que suele afirmar que las dos muestran tienen igual media porque proceden de la misma población. Cuando al realizar el contraste obtenemos significación (p<0.05) entonces rechazamos esta hipótesis nula (Ho) y aceptamos la alternativa (H1); esto es, que las medias son distintas tanto en cuanto que la probabilidad de que la diferencia hallada sea debida al azar es inferior al 5% (error alfa).
Para comparar medias entre dos muestras independientes seguimos el procedimiento Análisis à Comparar medias à Prueba T para muestras independientes, apareciendo el cuadro de diálogo siguiente:
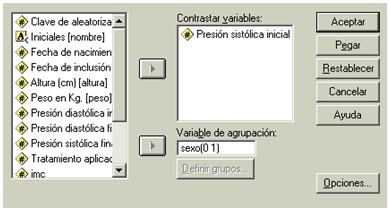
En este caso, tal como vemos, si nos interesa saber si la presión sistólica inicial de nuestra población es igual en varones que en mujeres, procede una T de Student para datos independientes. En la caja "contrastar variables" se introduce la v.a de la cual quiero comparar su media, por tanto, la variable cuantitativa. En la "variable de agrupación" tengo que introducir una única variable cualitativa o cuantitativa. Después pulsamos el botón "definir grupos" e introducimos los valores que puede tomar la variable de agrupación (en nuestro caso asignamos el 0 a mujeres y 1 a varones). Luego aceptar...y obtenemos una comparación de medias de presión sistólica en varones y mujeres, tal que así:
Estadísticos de grupo

Prueba de muestras independientes
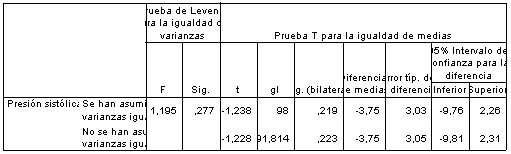
En la primera tabla obtenida encontramos el valor de la media, desviación típica y error estándar para la v.a presión arterial sistólica en los dos grupos (varones y mujeres). A continuación encontramos una segunda tabla que consta de dos grandes apartados:
Test de Levene: Se trata de conocer en primer lugar si las varianzas en ambos grupos son iguales o distintas, para lo cual se aplica este test. Como vemos la significación en Levene es 0.277, o sea, mayor de 0.05, por tanto no significativo, luego las varianzas son iguales.
Conocido que las varianzas entre grupos son iguales ya sé que en la prueba T (parte derecha de la tabla) tengo que leer sólo la columna "se han asumido varianzas iguales" y, leyendo esta columna veo que la significación p= 0.219 (>0.05) y por tanto no existen diferencias significativas de la presión arterial sistólica inicial en ambos grupos. Nos proporciona la tabla, además un intervalo de confianza para la diferencia de las medias halladas, en este caso el intervalo es [-9.76,2.26] y, como vemos, incluye al cero al no ser significativo el contraste (no incluirá al cero cuando el contraste sea significativo).
4. PRUEBA T PARA DOS MUESTRAS APAREADAS
Se aplica cuando los valores que toma la variable son medidos en la misma muestra pero en dos momentos distintos. En la base de ejemplo tenemos el dato "tensión arterial sistólica inicial" y " tensión arterial sistólica final", esto es, tras tomar un tratamiento. Se trata de una misma muestra, pero existen valores antes y después de la toma del medicamento. La comparación de medias bajo la premisa de medir la misma variable antes/después se realiza mediante la T de Student para datos apareados.
El procedimiento es Analizar à Comparar medias à T para muestras relacionadas, obteniendo el cuadro de dialogo siguiente:
variables_comparar.jpg
Hemos introducido las variables pas_ini y pas_fin en la caja de la derecha, posteriormente aceptar y se obtiene el resultado siguiente: (pas – presión arterial sistólica)
Estadísticos de muestras relacionadas

Prueba de muestras relacionadas
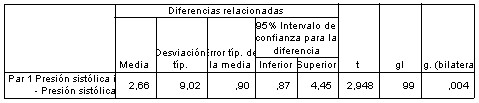
En la primera tabla vemos la media de ambas variables con su DT y EE. En la tabla inferior se presenta la significación para la diferencia (en este caso 0.04, sí significativo); la media para el valor de la diferencia [diferencia media] (2.66) acompañada de su EE (0.90) y el intervalo de confianza para la media de las diferencias halladas. Por tanto en este ejemplo podemos decir que existen diferencias significativas en la presión arterial antes y después de tomar el fármaco, que la media de las diferencias es de 2.66 mmHg con un EE 0.90, IC al 95% [0.87-4.45]. Notemos que el IC no incluye al valor 0 y de ello se desprende ya que existe significación.